快速入门
量子计算机工作原理
传统计算机采用来自于图灵和冯·诺依曼的经典计算模型进行信息处理。传统计算机芯片上集成有大量的晶体管,通过控制晶体管电压的电平高低,从而决定一个数据是“0”还是“1”。这种“0”或“1”的二进制数据模式被人们称作经典比特,经典比特在同一时间只能处于“0”或“1”其中之一的状态。这也就是说,在计算流程中的任意时刻,一个传统计算机的n个比特将处于2n个可能状态之一(从00……0到11……1)。
量子计算机采用的计算单元是量子比特。但是,与传统计算机的经典比特只能处于“0”或“1”的特定状态不同,量子比特可以处于|0>态、|1>态或者|0>和|1>线性组合而成的叠加态。此处量子比特的状态采用由保罗·狄拉克所定义的右矢符号|>来表示。当量子比特处于由|0>和|1>线性组合而成的叠加态时,在对应的基矢上对量子比特的状态进行测量将分别有一定的概率得到|0>或|1>,得到|0>或|1>的概率由线性叠加的系数决定。神奇的是,如果不对处于叠加态的量子比特进行测量,那么对量子比特所做的所有操作均相当于对量子比特可能处于的状态同时进行操作。
量子计算区别于经典计算的另一个特点来自于量子纠缠。简单地说,量子纠缠就是指当前的n个量子比特处于相互关联的状态,对其中一个比特进行测量将得知所有比特所处的状态,对其中一个比特进行操作将会改变所有比特所处的状态。量子纠缠赋予了量子计算机强大的计算潜能,也是量子计算机完全区别于传统计算机的关键。但是,正是由于量子计算所基于的物理原理与传统计算完全不同,需要针对量子计算机设计专用的量子算法(比如大数的质因子分解)才能体现其强大的算力优势。
名词解释
量子比特
量子比特(又称为Q比特、qubit ),在量子信息学中是量子信息的计量单位。传统电脑使用的是0和1,量子电脑虽然也是使用0跟1,但不同的是,量子电脑的0与1可以同时计算。
量子叠加
在古典系统中,一个比特在同一时间,只有0或1,不是0就是1,不是1就是0,只存在一种状态,但量子比特可以是1同时也可以是0,两种状态同时存在,这种效果叫量子叠加。这是量子电脑计算当前独有的特性。
量子门(量子逻辑门)
在量子计算和特别是量子线路的计算模型里面,一个量子门(或量子逻辑门)是一个基本的,操作一个小数量量子比特的量子线路。它是量子线路的基础,就像传统逻辑门跟一般数字线路之间的关系。
量子线路编辑器
用于进行量子线路编程的图形化界面,通过定义量子门及测量等操作来构建量子线路。
量子门词汇表说明
| 量子门 | 描述 |
|---|---|
| ID | 保持当前量子比特不变 |
| X | Pauli-X门,可使量子比特状态在|0>和|1>之间翻转 |
| Y | Pauli-Y门,以Bloch球上Y方向为轴旋转π角度 |
| Z | Pauli-Z门,以Bloch球上Z方向为轴旋转π角度 |
| H | Hadamard门,可使量子比特状态由|0>变为|+>或者由|1>变为|-> |
| S | 以Bloch球上Z方向为轴旋转π/2角度 |
| Sdg | 以Bloch球上Z方向为轴旋转-π/2角度 |
| SWAP | 交换两个量子比特的状态 |
| CX | 控制-非门,由控制比特和目标比特构成,当且仅当控制比特状态为|1>时翻转目标比特的状态 |
| Z measurement | 在Z基矢上测量单个量子比特的状态 |
快速创建量子线路
步骤一
进入量子计算服务页面,选择电路编程,点击创建电路编程。
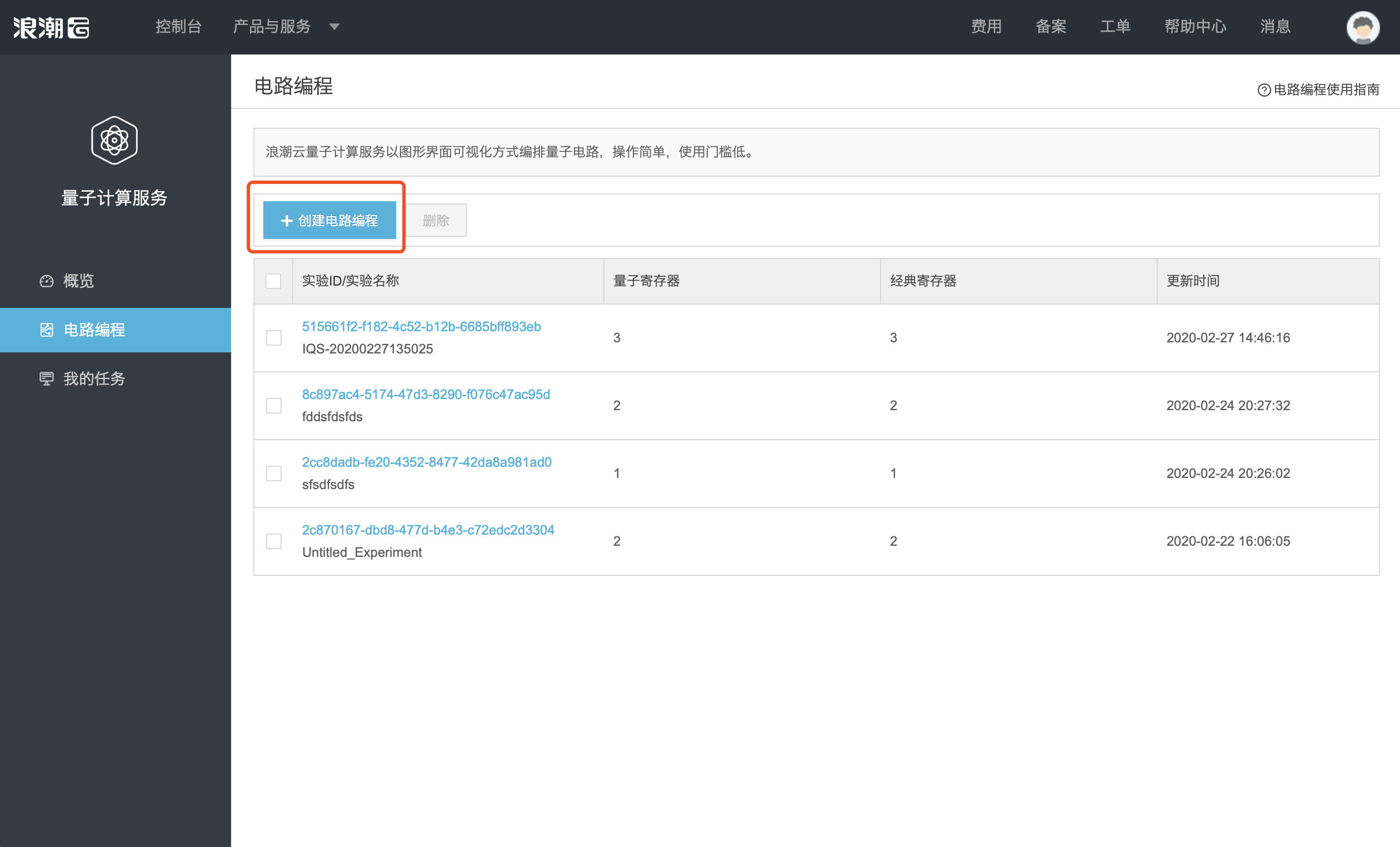
步骤二
完成对量子线路的基本配置,在量子线路编辑器(图形界面)上,拖拽量子门图标,完成量子线路。
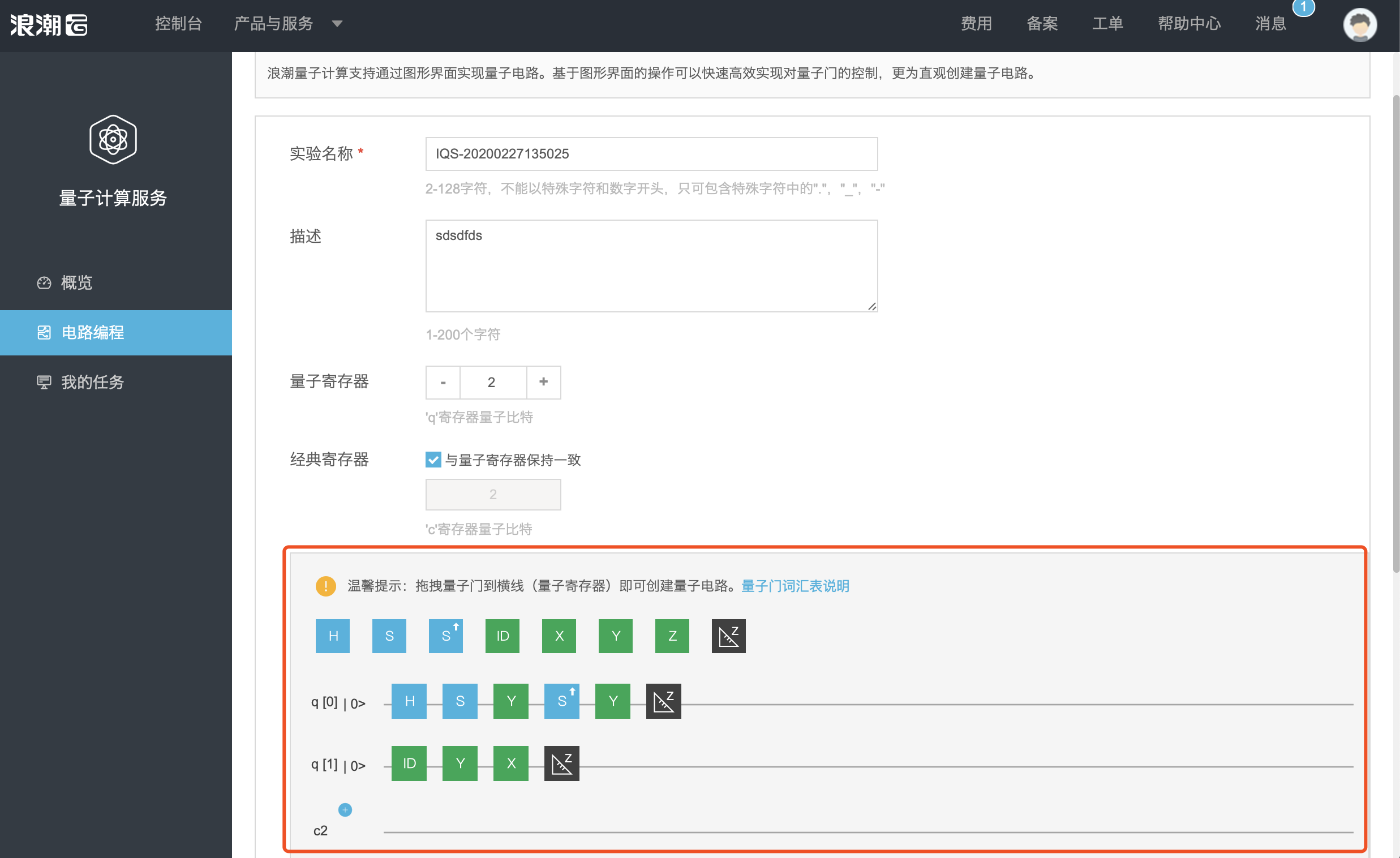
步骤三
点击运行,选择运行量子线路的量子计算机及shots数量后,点击确定。
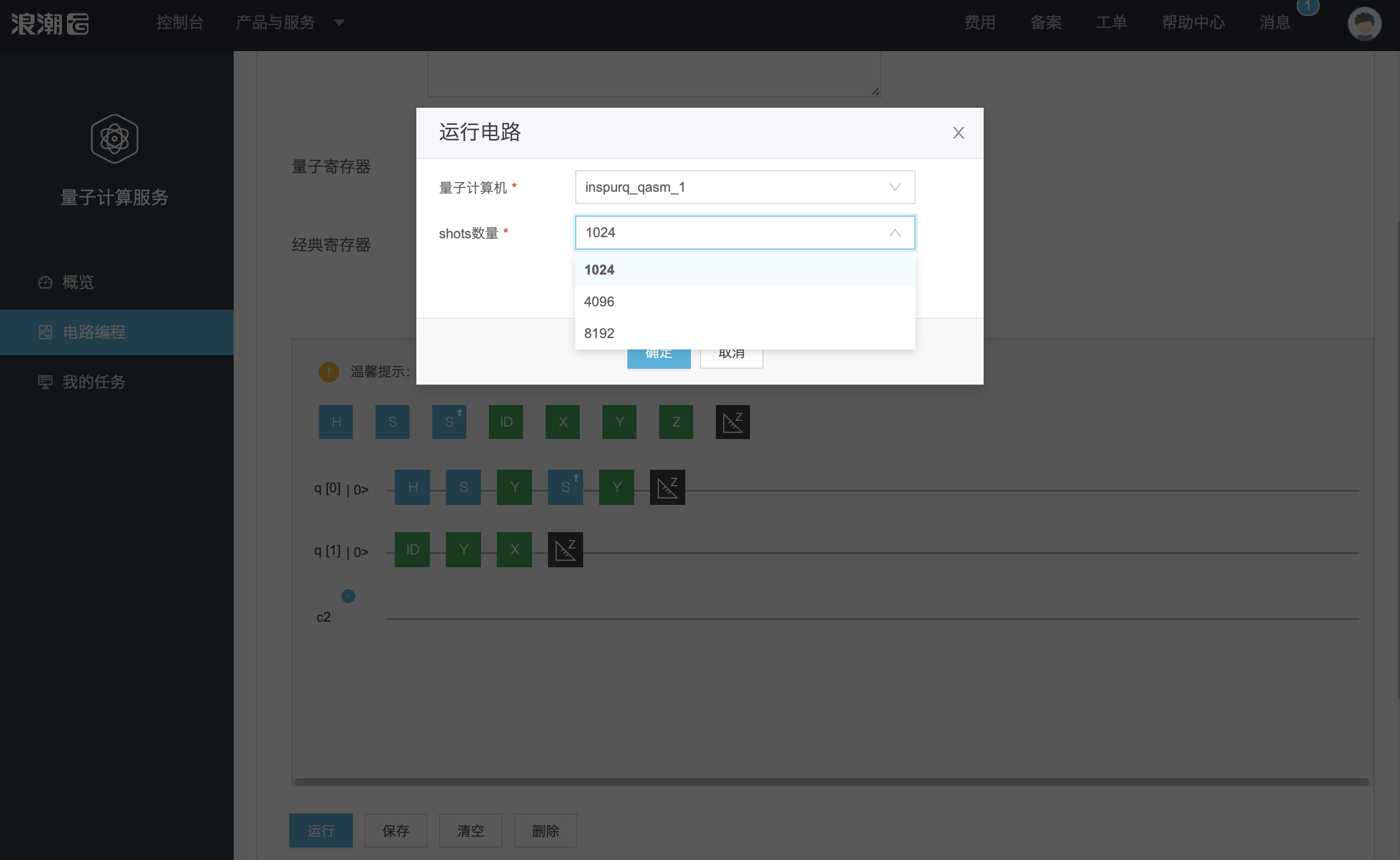
步骤四
选择我的任务页,选择任务列表,查看运行的任务的状态。
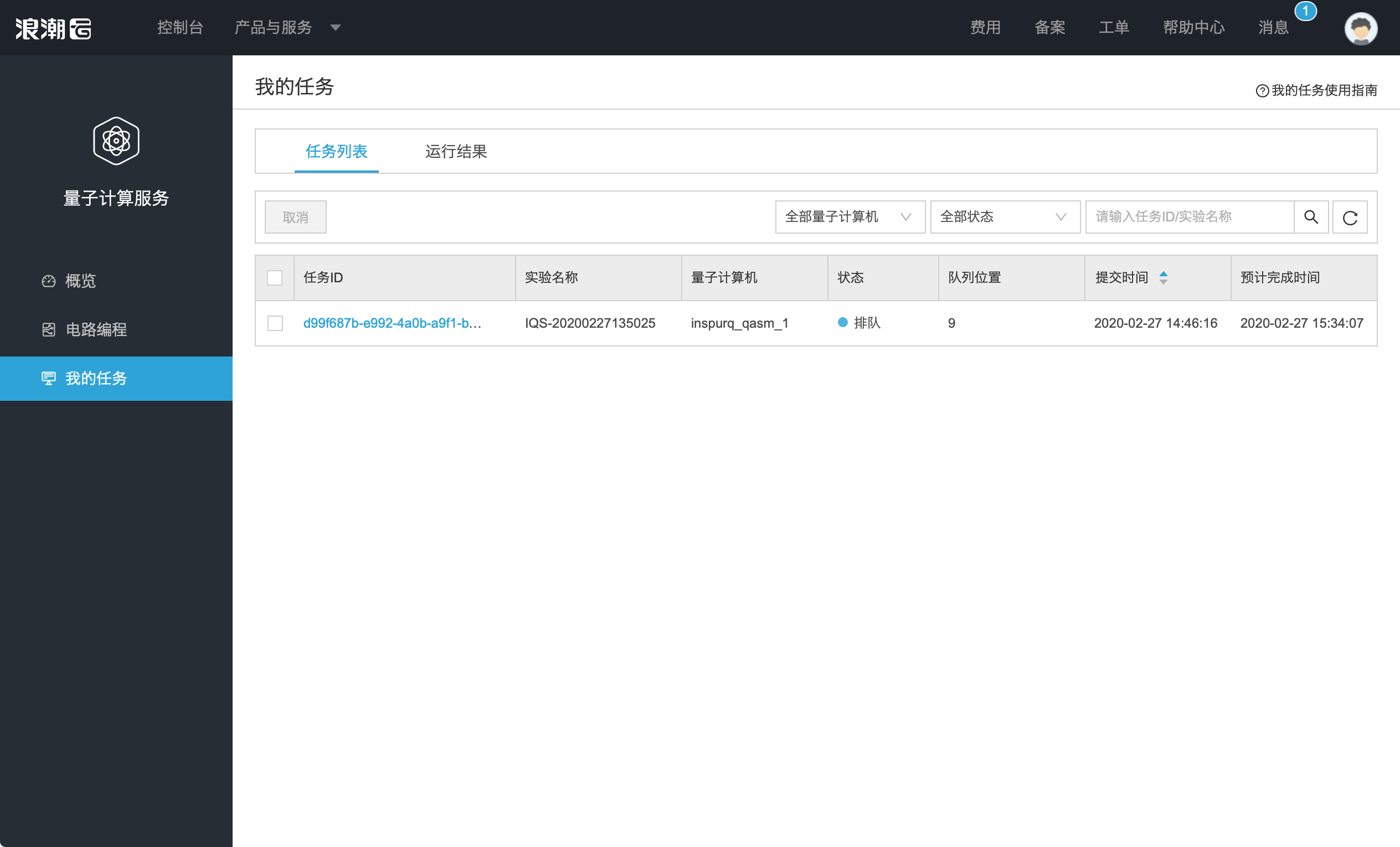
步骤五
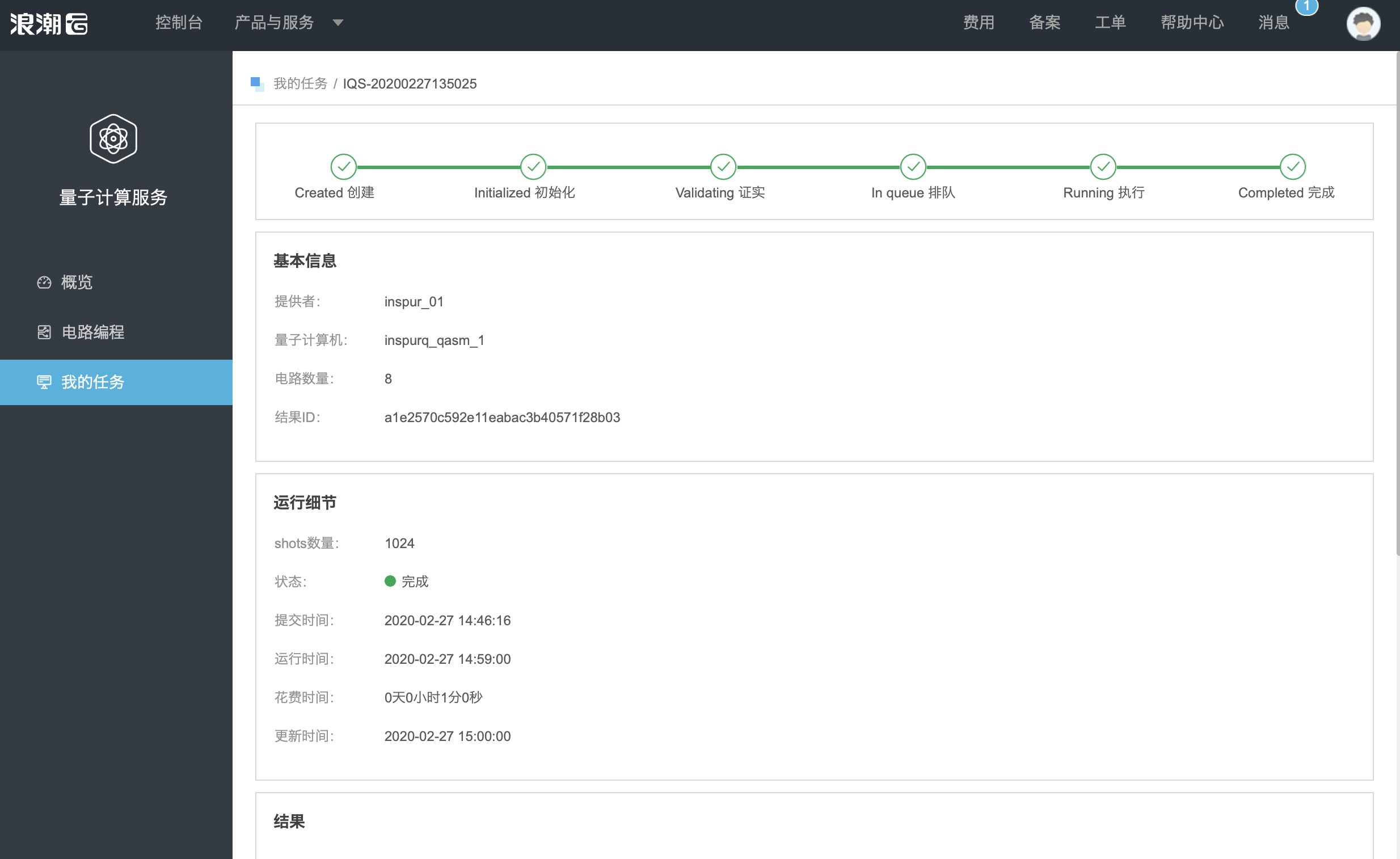
任务运行完成后,在我的任务页,选择运行结果,查看运行完成的结果列表。
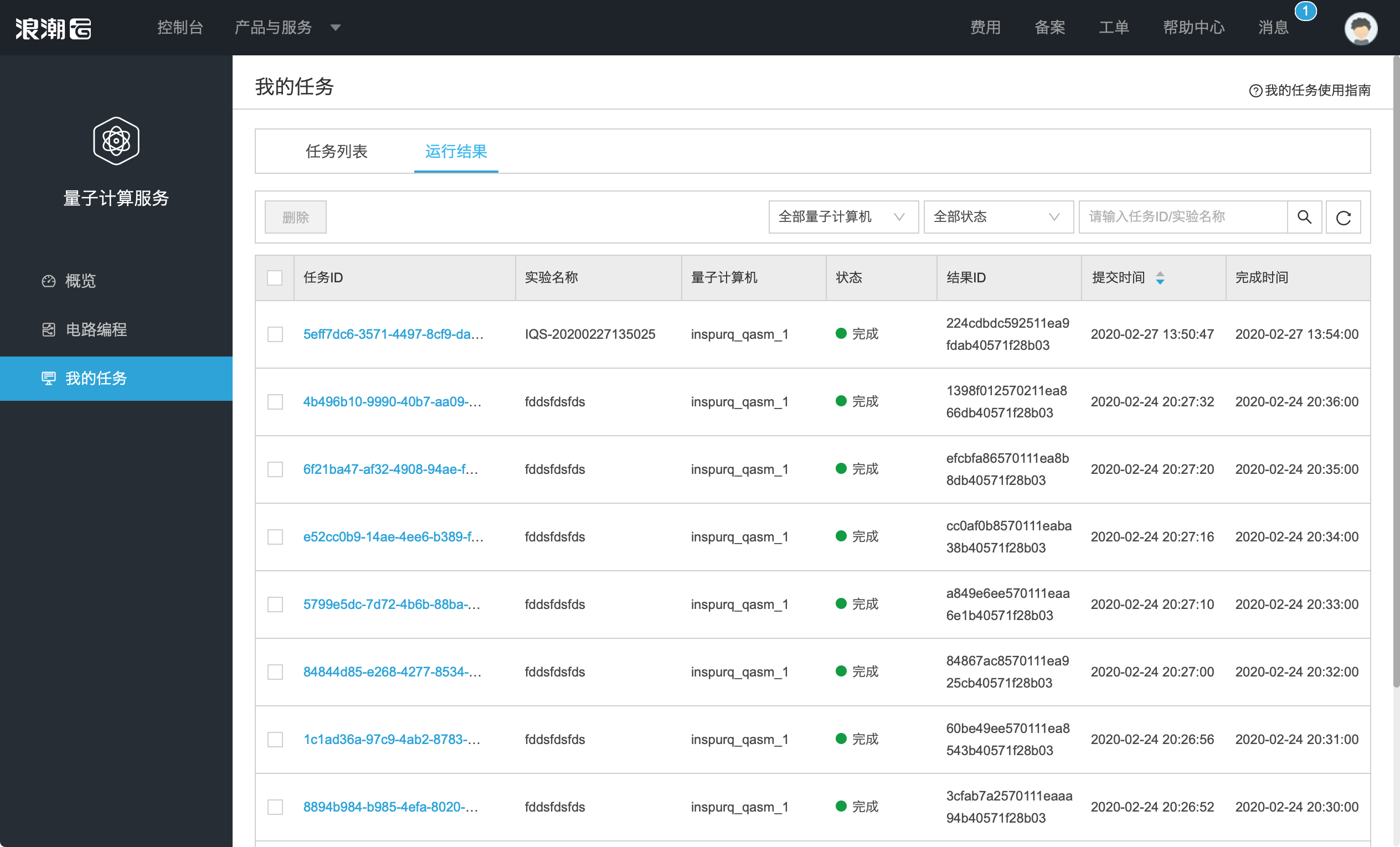
步骤六
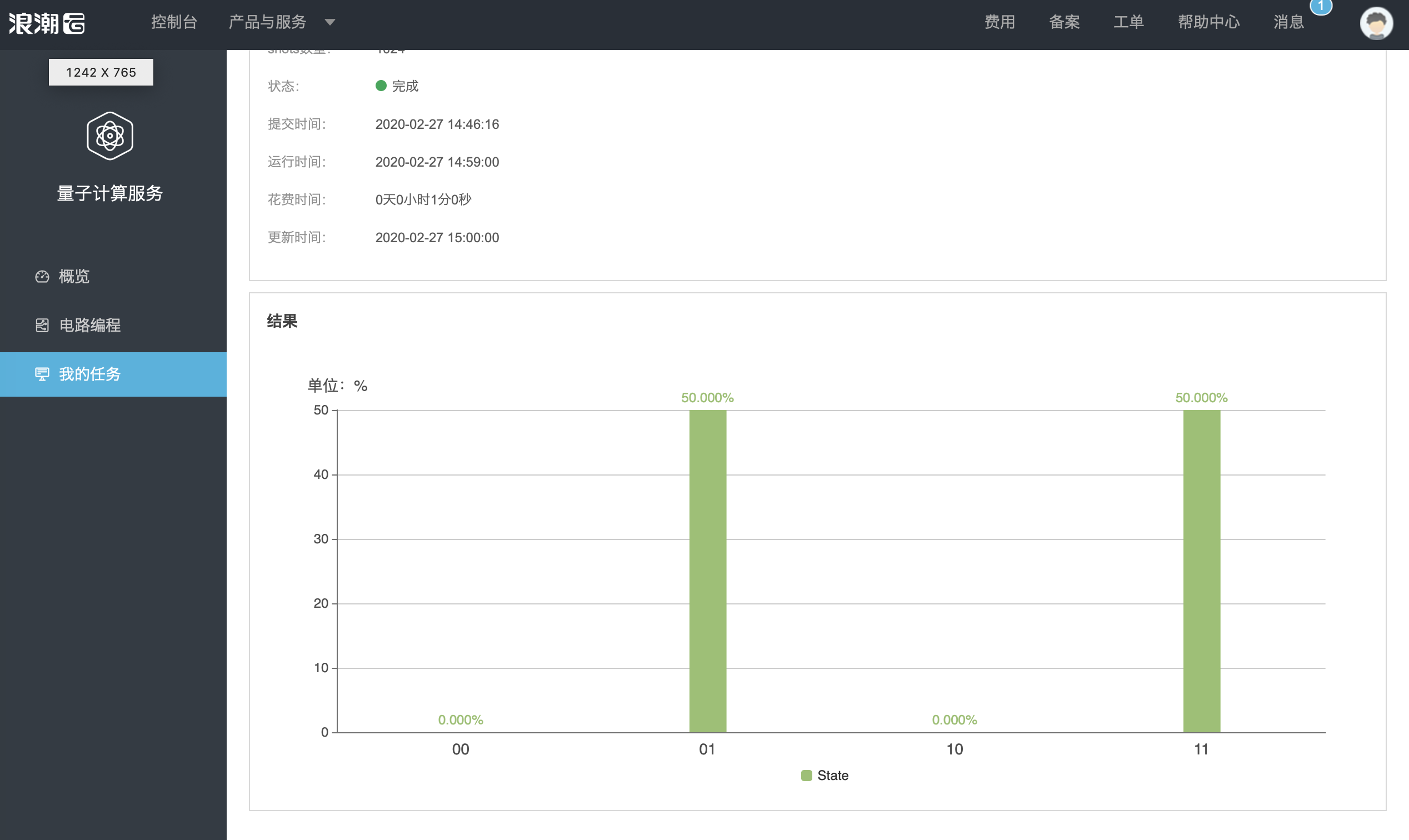
点击相应的结果的实验名称,可查看结果详情。
结果以柱状图的形式展现。